Research interests: I am interested in the construction and analysis
of Mathematical Models
for Geophysical Fluid Dynamics. You will find below a list of my
current research interests. My approach is characterised by the
construction of simplified mathematical models, which are sometimes tackled
numerically, sometimes with a joint asymptotic and numerical approach, yet
always motivated by real world problems.
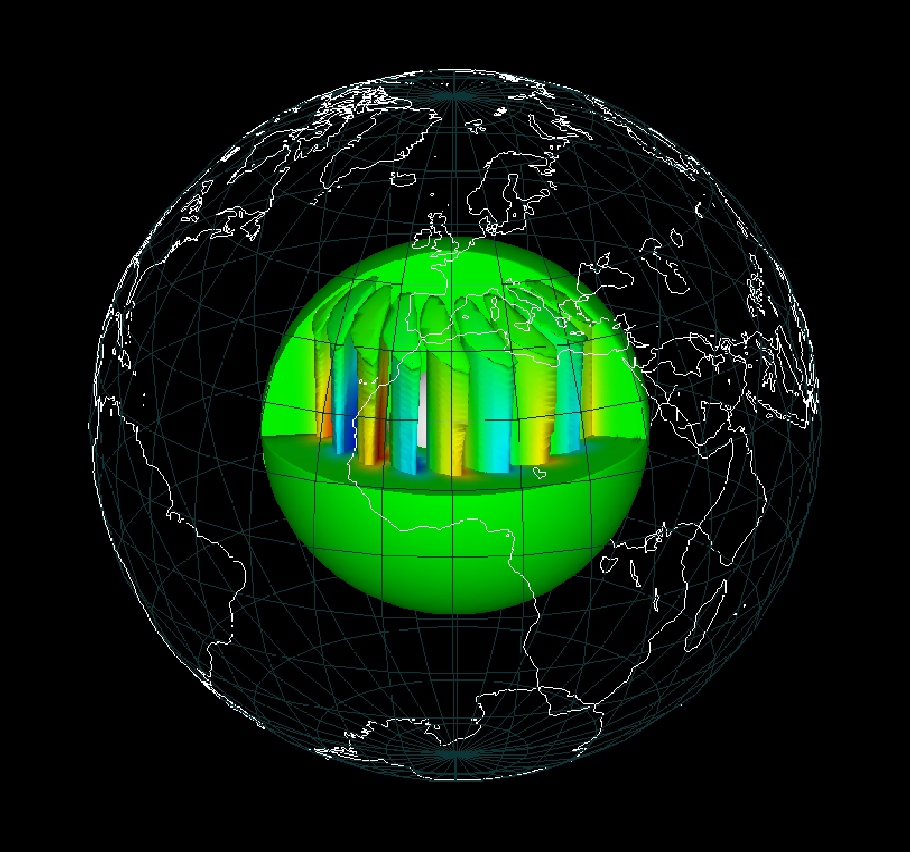 Numerical simulation of convection in the Earth
core
Numerical simulation of convection in the Earth
core
[E. Dormy]. I am interested in the understanding of natural
dynamos. The Earth core (approximatively 3000 km below our feet) consists
largely of liquid iron in convection.
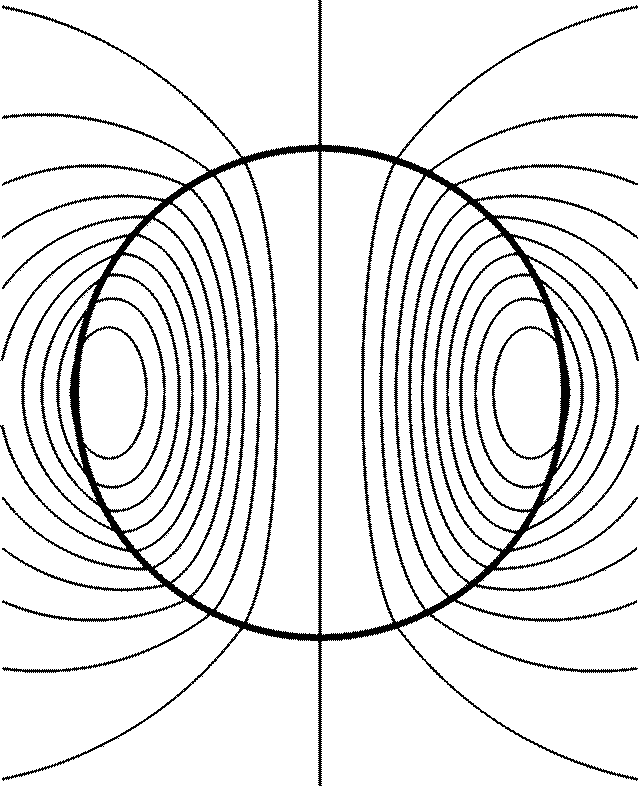 Slowest decaying mode in a conducting sphere [E. Dormy].
Slowest decaying mode in a conducting sphere [E. Dormy].
This convective flow is strongly
influenced by the rapid rotation of the Earth. The magnetohydrodynamic
flow in the core is thought to sustain a self excited dynamo, which
generates the main part of the Earth magnetic field. Although the geodynamo
theory was first proposed in 1919, the precise mechanism of the field
generation remains unknown. The same mechanism, although under different
conditions, is expected to account for the magnetic field of stars (like
the Sun) or even galaxies (like the Milkyway).
 Teahupoo, Tahiti [Picture
Teahupoo, Tahiti [Picture
E. Dormy]. Numerical simulation of wave breaking using the
vortex method
Numerical simulation of wave breaking using the
vortex method
[E. Dormy & C. Lacave]. Water waves at the surface of the ocean are familiar to
everyone. Surprisingly several fundamental issues remain open concerning their
generation, their evolution and their interaction with the
environment.
Possibly one of the most striking property of water waves is their
ability to develop a sharp singularity from an initially smooth
configuration. This is known as the
wave breaking problem, which raises
serious mathematical difficulties.
Wave breaking often occurs as the waves approach land and the depth of
water
reduces, as the waves slows down, its amplitude increases; it can however also occur away from the coast.
 Tropical Cyclone Maysak (2015)
[Picture T. Virts from the ISS].
Tropical Cyclone Maysak (2015)
[Picture T. Virts from the ISS].
Tropical Cyclones (TCs) are among the most deadly and destructive natural
disasters on Earth, they are certainly the most energetic structures in
the atmosphere. They present a large number of fascinating and unresolved
problems.
One of their most striking features
is that they develop a so-called eye:
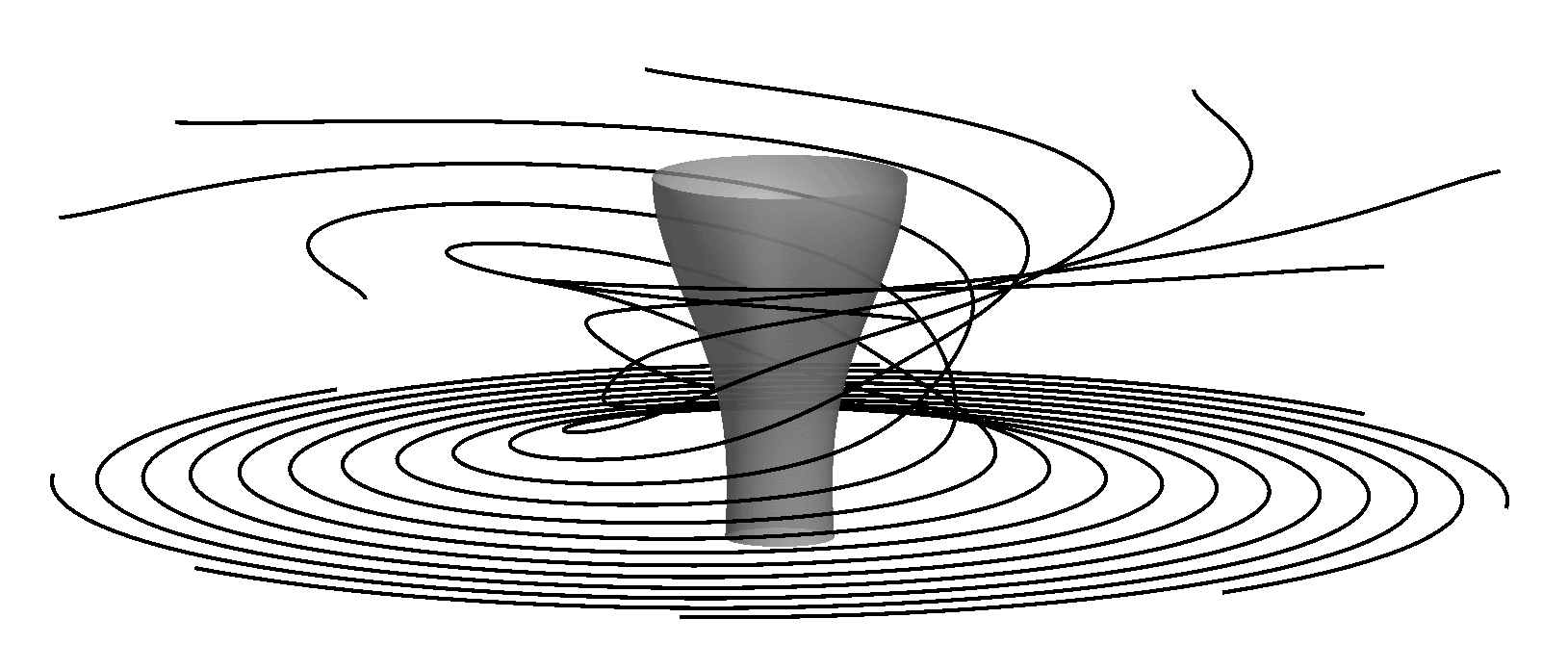 Sketch
of a Tropical Cyclone (model of Oruba, Davidson,
Dormy, JFM, 2017).
Sketch
of a Tropical Cyclone (model of Oruba, Davidson,
Dormy, JFM, 2017).
a region of reversed flow in and around
the axis of the vortex.
Much has been written about eye formation
in the context of tropical cyclones, but the key dynamical processes are still
poorly understood.
I am working on this question as well as that of the rapid intensification
often observed for tropical cyclones and which hinders the prediction of
their consequences.
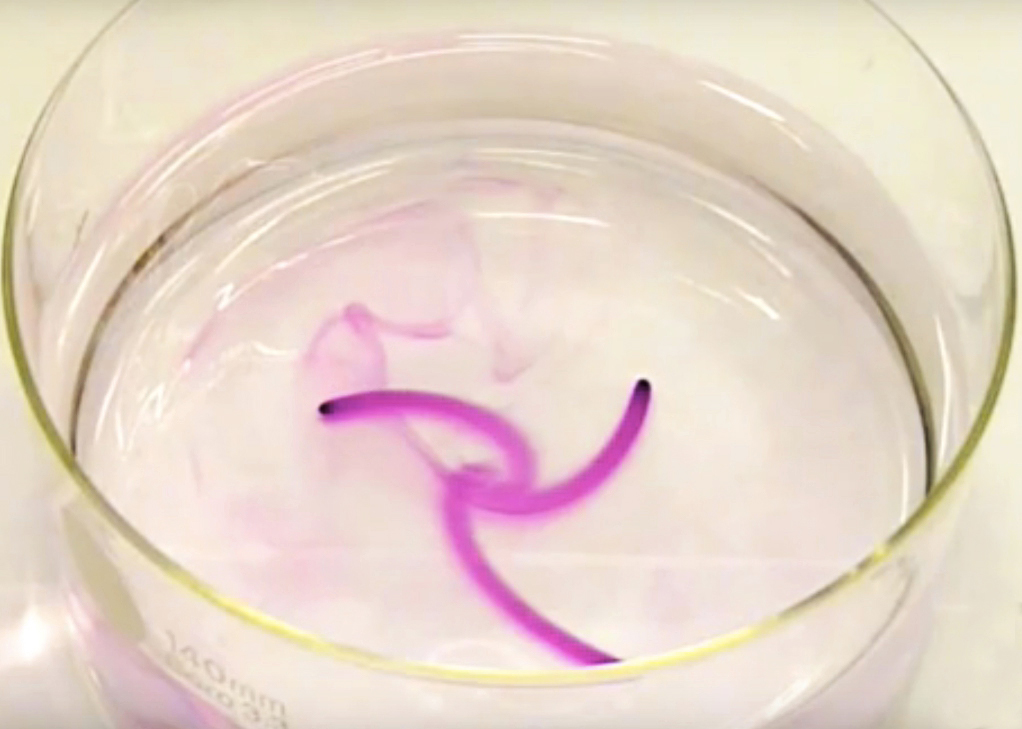 "Tea Cup Experiment", click on the picture!
"Tea Cup Experiment", click on the picture!
[Mazelet & Dormy] 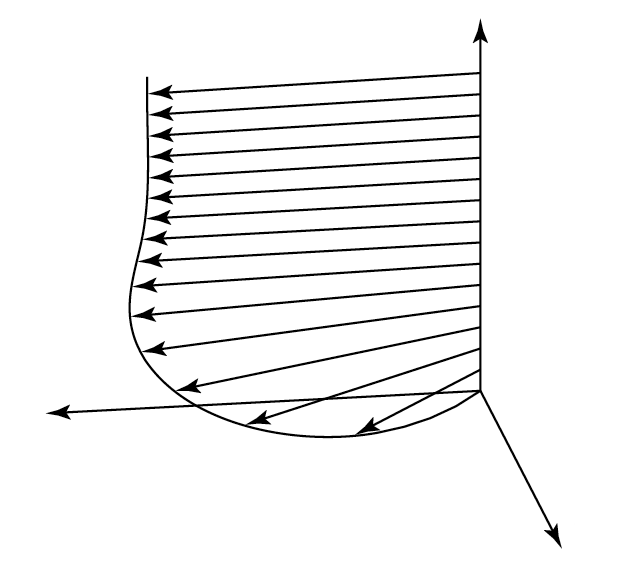 Flow in the Ekman layer (after Dormy & Soward, 2007).
Flow in the Ekman layer (after Dormy & Soward, 2007). A key characteristic of geophysical fluids is the
role played by the rotation of the Earth on their dynamics. Fluid dynamics
in a non-inertial frame of reference is characterised by an additional term
in the Navier-Stokes equation, known as the
Coriolis term. Rotating
fluids are full of surprises and the flow is
often very counterintuitive.
 The DTS experiment in Grenoble.
The DTS experiment in Grenoble.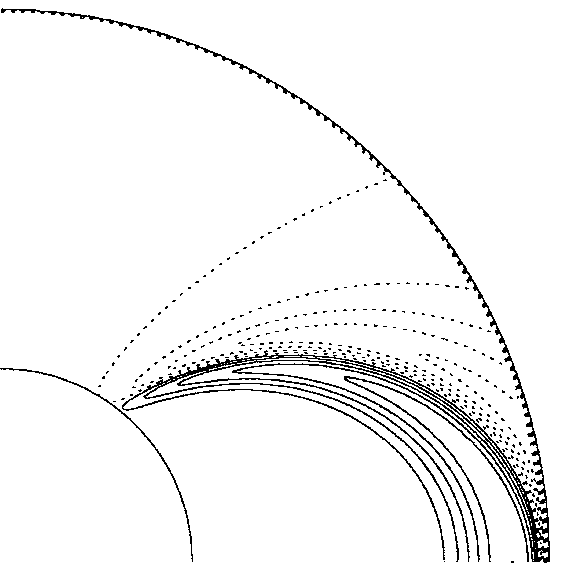 MHD shear layer in super-rotation
(introduced in Dormy et al. 1998).
MHD shear layer in super-rotation
(introduced in Dormy et al. 1998). (or MHD) consists in the study of flows in
conducting liquids. The most extreme case, of dynamo action has been
mentioned above. I am also interested in general in flows of liquid metal
and understanding how the Lorentz force affects the dynamics of the fluid.
MHD flows are often characterised by very thin shear layers, which raise
mathematical and numerical difficulties.
 Super-computer at one of the french national
computing centers (CCRT).
Super-computer at one of the french national
computing centers (CCRT). The study of the above problems, as well as many others
in fluid dynamics, can benefit from efficient numerical simulations.
Such
simulations are only useful when they can be interpreted physically. This
is often achieved through detailed comparisons with theoretical or
experimental work. This requires high resolution simulations, varying
parameters significantly. I am interested in the development of efficient
numerical methods to allow such comparisons.
Asymptotic expansions can in some cases provide exact analytical solutions,
usually in the form of special function expansions; however in many cases
the asymptotic equations cannot be solved analytically,
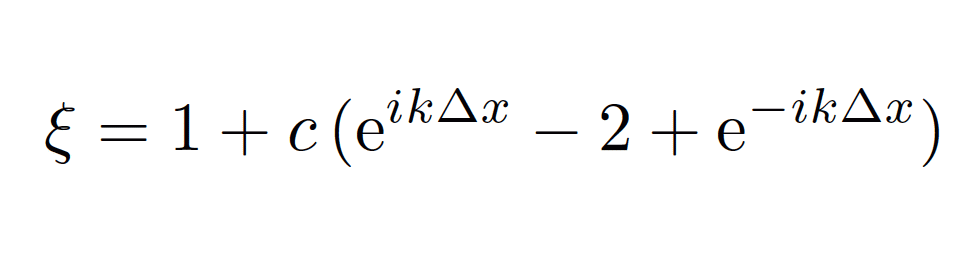 Von Neumann amplification factor for the heat equation with an explicit Euler scheme.
Von Neumann amplification factor for the heat equation with an explicit Euler scheme.
and progress is
only possible by numerical solution. This is far from straightforward:
often regularising terms (such as viscous effects) are retained in one
direction only (normal to a shear say) and great care must be taken in
choosing the numerical scheme and building the resolution algorithm, in
order to guarantee numerical stability.
 Numerical simulation of convection in the Earth
core
Numerical simulation of convection in the Earth
core Slowest decaying mode in a conducting sphere [E. Dormy].
Slowest decaying mode in a conducting sphere [E. Dormy]. Teahupoo, Tahiti [Picture
Teahupoo, Tahiti [Picture Numerical simulation of wave breaking using the
vortex method
Numerical simulation of wave breaking using the
vortex method Tropical Cyclone Maysak (2015)
[Picture T. Virts from the ISS].
Tropical Cyclone Maysak (2015)
[Picture T. Virts from the ISS]. Sketch
of a Tropical Cyclone (model of Oruba, Davidson,
Dormy, JFM, 2017).
Sketch
of a Tropical Cyclone (model of Oruba, Davidson,
Dormy, JFM, 2017). Flow in the Ekman layer (after Dormy & Soward, 2007).
Flow in the Ekman layer (after Dormy & Soward, 2007). The DTS experiment in Grenoble.
The DTS experiment in Grenoble. MHD shear layer in super-rotation
(introduced in Dormy et al. 1998).
MHD shear layer in super-rotation
(introduced in Dormy et al. 1998). Super-computer at one of the french national
computing centers (CCRT).
Super-computer at one of the french national
computing centers (CCRT).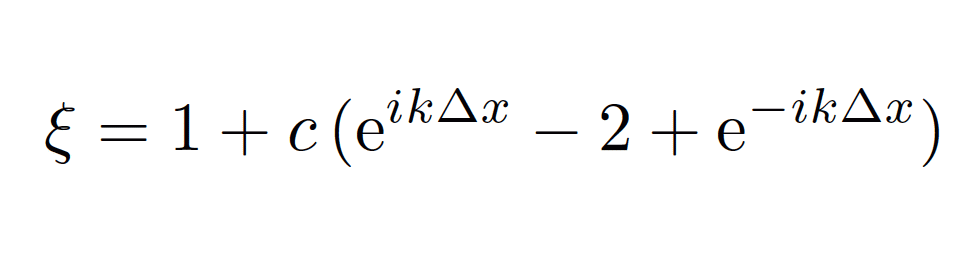 Von Neumann amplification factor for the heat equation with an explicit Euler scheme.
Von Neumann amplification factor for the heat equation with an explicit Euler scheme.







